Text
Unit D2 Section 3
Use of Tree Diagrams

Tree diagrams can be used to find the probabilities for two events, when the outcomes are not necessarily equally likely.

Worked Examples

1

If the probability that it rains on any day is , draw a tree diagram and find the probability

The tree diagram shows all the possible outcomes. Then the probability of each event can be placed on the appropriate branch of the tree. The probability of no rain is 1 − = .

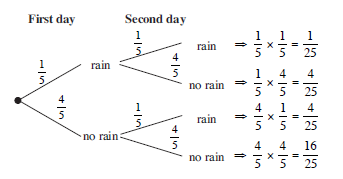
The probability of each outcome is obtained by multiplying together the probabilities on the branches leading to that outcome. For rain on the first day, but not on the second, the probability is

× =

(a)

that it rains on two consecutive days,

The probability that it rains on two consecutive days is given by the top set of branches, and is .
(b)

that it rains on only one of two consecutive days.

There are two outcomes where there is rain on only one of the two days. These are rain – no-rain, with a probability of and no-rain – rain with a probability of .

The probability of rain on only one day is found by adding these two probabilities together:

+ =

2

The probability that Jenny is late for school is 0.3. Find the probability that on two consecutive days she is:

The tree diagram shows the possible outcomes and their probabilities. Note that the probability of not being late is   1 − 0.3 = 0.7.

The probabilities on each set of branches are multiplied together to give the probability of that outcome.

(a)

never late,

The probability that Jenny is never late is given by the bottom set of branches and has probability 0.49.
(b)

late only once.

The probability that she is late once is given by the two middle sets of branches which both have a probability 0.21. So the probability that she is late once is given by

0.21 + 0.21 = 0.42

Note

The method shown here also works for problems when the outcomes are equally likely (as in the previous method) – it is sometimes rather cumbersome though to draw all the branches.

The next example is the same as Worked Example 2 in Section D2.2, but this time the tree diagram method will be used.

3

A spinner that forms part of a children's game can point to one of four regions, A, B, C or D, when spun. What is the probability that when two children spin the spinner, it points to the same letter?

This time, let us use the tree diagram approach.

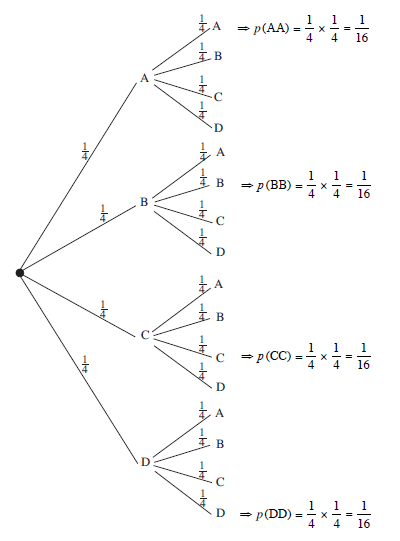
So the probability of both children obtaining the same letter is

+ + + = (as obtained before)

Exercises

On a route to a factory a truck must pass through two sets of traffic lights. The probability that the truck has to stop at a set of lights is 0.6.

(a)

What is the probability that the truck does not have to stop at a set of traffic lights?

(b)

Copy the tree diagram below and add the correct probabilities to each branch.

× =
× =
× =
× =
(c)

What is the probability that the truck gets to the factory without having to stop at a traffic light?

(d)

What is the probability that the truck stops at both sets of traffic lights?

(e)

What is the probability that the truck stops at one set of traffic lights?

Two boys are playing a game. They take it in turns to start. Before they start they must throw a six. John starts first.

(a)

What is the probability of throwing a six?

(b)

Copy the tree diagram and add the appropriate probabilities to each branch.

Also calculate the probability of each outcome shown on the tree diagram.

× =
× =
× =
× =
(c)
Find the probability that:
(i)
both boys start the game on their first throws,
(ii)
only one of them starts the game on their first throw,
(iii)
neither of them starts the game on their first throw.

Mike travels to Swindon from Bristol on the early bus. The probability that he arrives late is . He catches the bus on two consecutive days.

What is the probability that he arrives:

(a)
on time on both days,
(b)
on time on at least one day,
(c)
late on both days.

When Sheila's office phone rings the probability that the call is for her is .

(a)

What is the probability that a call is not for Sheila?

Draw a tree diagram that includes probabilities to show the possible outcomes when the phone rings twice.
(b)

Find the probabilities that:

(i)
both calls are for Sheila,
(ii)
only one call is for Sheila,
(iii)
neither call is for Sheila.

In a school canteen the probability that a student has fries with their meal is 0.9 and the probability that they have beans is 0.6.

(a)

Copy and complete the tree diagram below.

(b)
What is the probability that a student has:
(i)
both fries and beans,
(ii)
fries but not beans,
(iii)
neither fries nor beans?

To be able to drive a car unsupervised you must pass both a theory test and a practical driving test. The probability of passing the theory test is 0.8 and the probability of passing the practical test is 0.6.

(a)

What is the probability of failing:

(i)
the theory test,
(ii)
the practical test?
(b)

What is the probability that someone:

(i)
passes both tests,
(ii)
fails both tests?

Victoria calls for her friends, Kina and Freya. The probability that Kina is not ready to leave is 0.2 and the probability that Freya is not ready is 0.3.

Use suitable tree diagrams to find the probability that:

(a)
both Freya and Kina are ready to leave,
(b)
one of them is not ready to leave,
(c)
Kina is not ready to leave on two successive days,
(d)
Kina is ready to leave on two consecutive days.

A die has 6 faces of which 3 are green, 2 yellow and 1 red.

Find the probabilities of the following outcomes if the die is rolled twice.

(a)
Both faces have the same colour.
(b)
Both faces are red.
(c)
Neither face is green.

Mervin has 8 red socks and 6 white socks all mixed up in his sock drawer.

He takes 2 socks at random from the drawer.

(a)

If the first sock that Mervin takes is red, what is the probability that the second sock will also be red?

(b)

What is the probability that Mervin will take 2 socks of the same colour?